Hexagon Rendering

March 28, 2025

A procedural field of hexes (shader link).

Introducing Proximity

You are making a turn based strategy game with a hexagonal landscape. To get started, you whip up a procedural hex renderer. You decide you want to have spaces between the hexes, and need to detect whether the user's mouse is in a hex or a space. Oddly enough, the proper execution of any of these 3 ideas requires a mathematical concept I have never seen explicitly defined.

In this article, I will propose the concept of hex proximity, or the normalized proximity of a point in a hex to a boundary between hexes. I will showcase its use in both gameplay and procedural rendering, and I will relate it to well-known abstractions in both domains.

Also, at the end you will understand the toHex() function in the above shader!

Hexes In Gameplay

In truth, I have written this article in order to preamble endlessly about my favorite coordinate system. My first (decent) game took place on a hexagonal board, and I had the good fortune to read RedBlobGames' seminal interactive essay on 3-dimensional hex coordinates (which I will hereafter refer to as hex space or cube coordinates). Not only is it perfect for backend logic like pathfinding, I find the transformation from hex space to world space and back immensely gratifying. A common use-case, given by RedBlob in the article, is identifying which hexagon the user's mouse is hovering over.

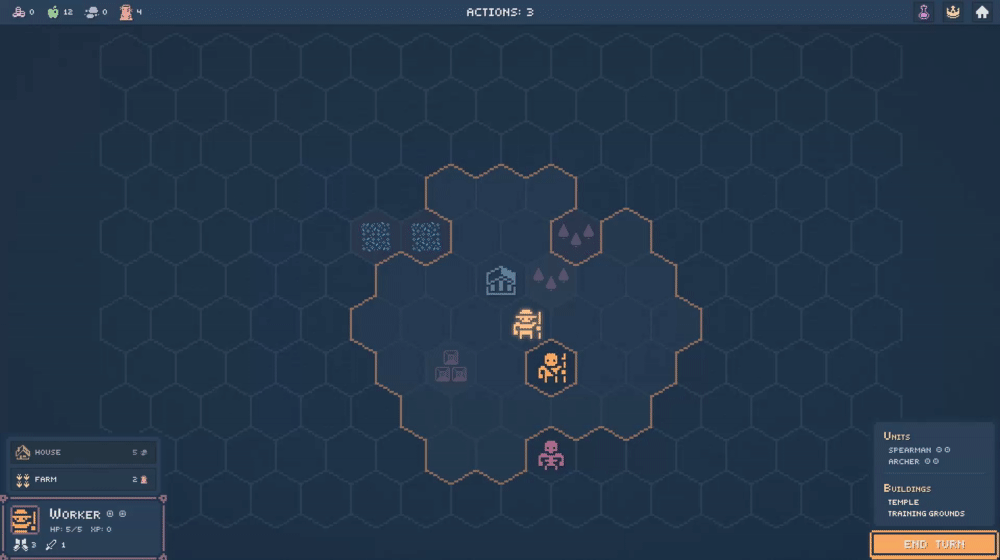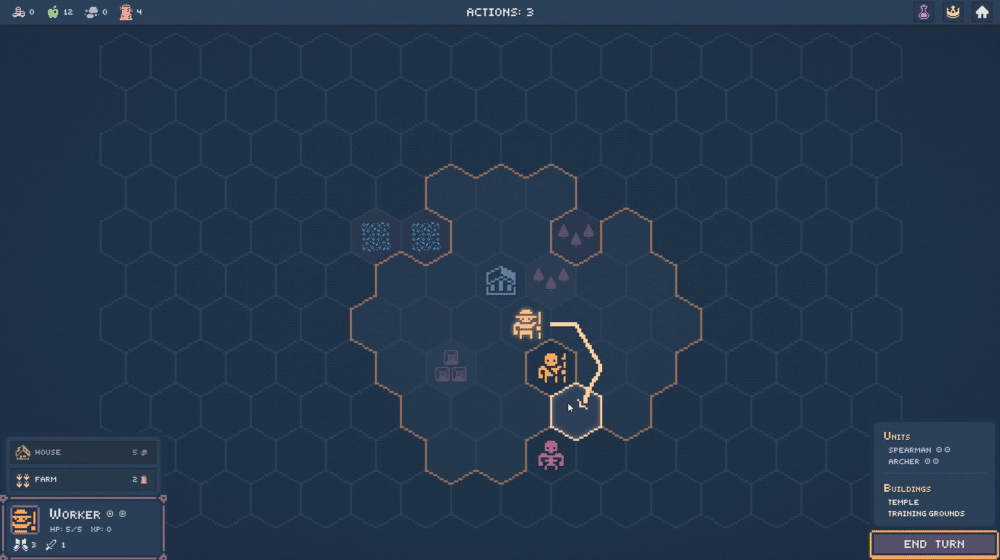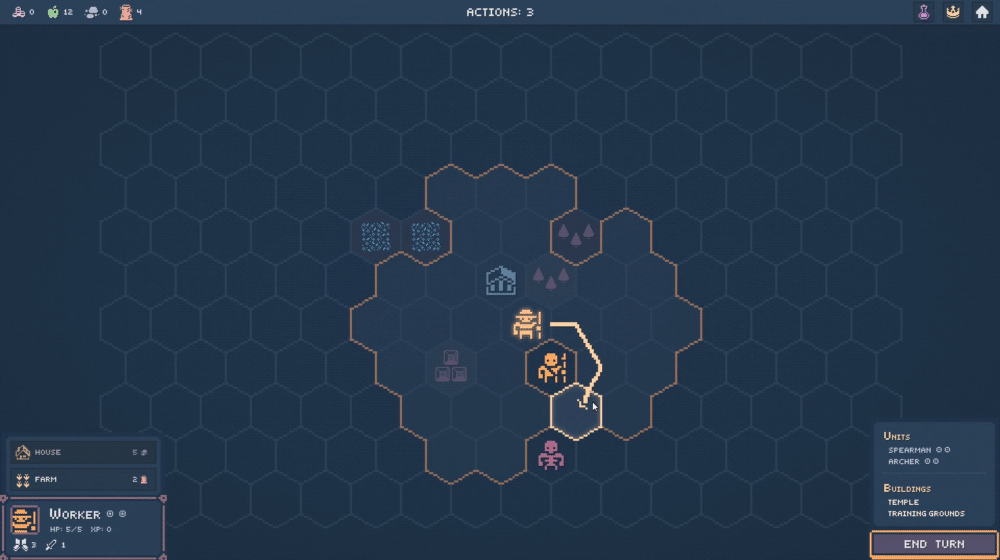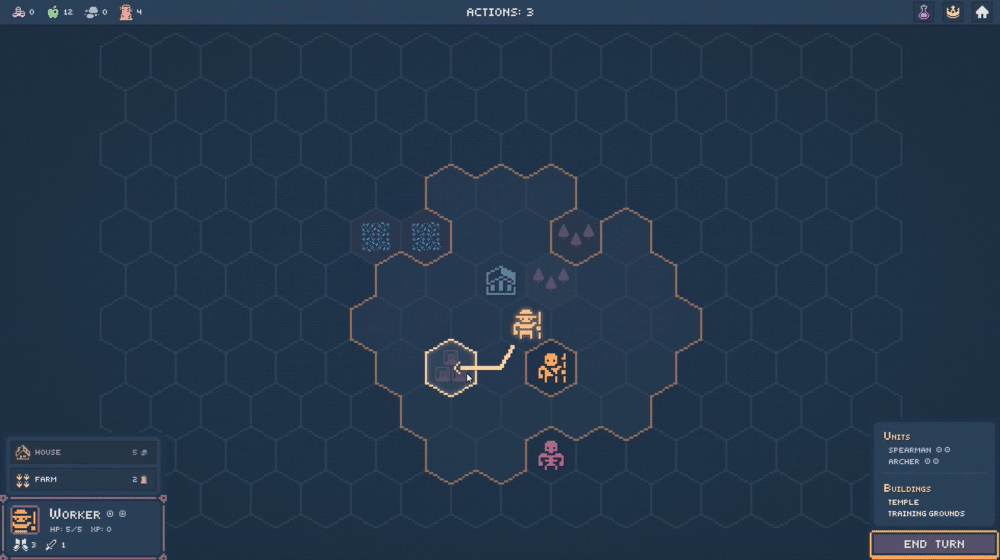Hexagons being moused-over in a recent strategy prototype.

Here is a simple rect-to-hex function, derived from the base-vectors of a hex (which are 60 degrees apart). Note that gameplay examples will be in C#, with pointy-top hexes (I use different base vectors than RedBlob's... sorry):

public static Vector2 RectToHex(Vector2 rectPos)
{
    Vector2 hexCoords = new Vector2
    (
        rectPos.x * SQRTOFTHREE / 3f - rectPos.y / 3f, // Q
        rectPos.y * 2f / 3f                            // R
    );
    return hexCoords;
}

As RedBlob notes, this produces a non-integer point in hex space. To achieve our goal of identifying the moused-over hex, we need to find the nearest integer value in hex space, which is accomplished by rounding and selecting the nearest legal cube coordinates.

public static HexCoord Round(Vector2 floatCoords)
{
    Vector3 cubeCoords = new Vector3(floatCoords.x, floatCoords.y,
        -floatCoords.x - floatCoords.y);
    
    int rQ = Mathf.RoundToInt(cubeCoords.x);
    int rR = Mathf.RoundToInt(cubeCoords.y);
    int rS = Mathf.RoundToInt(cubeCoords.z);
    
    float q_diff = Mathf.Abs(rQ - cubeCoords.x);
    float r_diff = Mathf.Abs(rR - cubeCoords.y);
    float s_diff = Mathf.Abs(rS - cubeCoords.z);
    
    if (q_diff > r_diff && q_diff > s_diff)
    {
        rQ = -rR - rS;
    }
    else if (r_diff > s_diff)
    {
        rR = -rQ - rS;
    }
    else
    {
        rS = -rQ - rR;
    }
    
    return new HexCoord(rQ, rR);
}

If you are not familiar with hex space, or are currently confused, I suggest reading the aforementioned article before continuing!

...

Now that you are brimming with understanding, we can return to our hypothetical spaced hexes, and "proximity". How do you know if a point is inside a hex that is, say, at 80% scale? Testing in world-space does us no good, since distance in world space is circular... What we need to know is how close we are to the boundary between hexes.

World space distance is unhelpfully circular... Identifying that the yellow point is outside the hex and the red one is inside will require a hex-space definition (interactive shader link).

Deriving Proximity

The goal now is to take advantage of the logic already built-in to the Round function, which selects the cube coordinate (q, r, s) which was "rounded the most" to be discarded. If we instead select the coordinate which is "rounded the least", we can use that to select an axis for measuring "proximity". Remember that proximity is a distance to the nearest hex boundary, and that hex boundaries are lines, so once we can construct a vector to project our point onto, we can easily measure the result.

Which boundary is nearest? Which axes to use?

How do we select our to_boundary vector with just (q_diff, r_diff, s_diff)? Looking at the above basis vector diagram, we can see that the nearest axis is the one with the largest diff (in this case q_diff). In the above example, q_diff is largest, and s_diff is smallest. The subtriangle we want is thus described by the Q and -R basis vectors.

We want to project our local point onto the vector from center to boundary.

To find the distance to the boundary, we want to project onto the vector (Q - R) / 2, which points from the center to the boundary. Because of the hexagon rule Q + R + S == 0, we can substitute -(S + R) for Q, producing -(S / 2 + R), and then we knock the minus sign off because our "diffs" are absolute values. So if s_diff is smallest and q_diff is largest, proximity = r_diff + .5 * s_diff.

Here is our updated round function, now also calculating proximity:

/// <param name="proximity">
/// This is a value representing proximity to a boundary between hexes
/// (0 is hex center, .5 is boundary), in cube coordinate space.
/// </param>
public static HexCoord Round(Vector2 floatCoords, out float proximity)
{
    Vector3 cubeCoords = new Vector3(floatCoords.x, floatCoords.y,
        -floatCoords.x - floatCoords.y);

    int rQ = Mathf.RoundToInt(cubeCoords.x);
    int rR = Mathf.RoundToInt(cubeCoords.y);
    int rS = Mathf.RoundToInt(cubeCoords.z);

    float q_diff = Mathf.Abs(rQ - cubeCoords.x);
    float r_diff = Mathf.Abs(rR - cubeCoords.y);
    float s_diff = Mathf.Abs(rS - cubeCoords.z);
    
    if (q_diff > r_diff && q_diff > s_diff) // if q_diff is largest
    {
        rQ = -rR - rS;
        if (r_diff < s_diff) // r_diff is smallest change. Project w/ s and r
        {
            proximity = s_diff + .5f * r_diff;
        }
        else
        {
            proximity = r_diff + .5f * s_diff;
        }
    }
    else if (r_diff > s_diff)
    {
        rR = -rQ - rS;
        if (q_diff < s_diff)
        {
            proximity = s_diff + .5f * q_diff;
        }
        else
        {
            proximity = q_diff + .5f * s_diff;
        }
    }
    else
    {
        rS = -rQ - rR;
        if (q_diff < r_diff)
        {
            proximity = r_diff + .5f * q_diff;
        }
        else
        {
            proximity = q_diff + .5f * r_diff;
        }
    }

    return new HexCoord(rQ, rR);
}

You may notice I have specified that proximity == 0 means the point is at the center of the hex, and proximity == .5 means it is on the boundary. But why .5? The reason is to maintain consistency with hex space: 1 is the distance between two adjacent hex centers. Thus, proximity is analogous to a "remainder" after rounding to the nearest hex. I also find it interesting that if proximity == .5, then the furthest, discarded coordinate of (q_diff, r_diff, s_diff) must also be .5, as round_remainder() can give no higher values.

I almost forgot! We're trying to identify whether a point is inside an 80%-scale hexagon! Well, let's see... is 2. * proximity < .8? Simple as that!

Points inside and outside 80%-scale hexagons (shader link).

It's easy to see, I hope, that this function has applications beyond detecting hex mouseovers. It provides a continuous function mapping any point in world space to our new proximity concept! In the next section I will demonstrate my favorite use-case for such a function: procedural rendering.

Proximity In Rendering

Time to draw some hexagons! Our proximity function describes the distance to a boundary. In the procedural rendering world, that can only mean one thing: a Signed Distance Field (SDF). As in the previous section, I will be extending a well-established framework, so I adjure you to make reference to this highly regarded procedural rendering tutorial.

A distance function for a box (shader link, credit to IQ).

For our purposes, an SDF is any function (or texture, as in the famous Valve paper which popularized SDF font rendering) which tells us how far our pixel is from the line or solid area we want to draw. If the SDF says our pixel is inside (aka negative distance), we draw. If it says outside (aka positive distance), we don't draw. A big advantage of the technique is at the boundary (aka near 0), where we can do free anti-aliasing, since by definition we know how close to the boundary our pixel is.

A simple example of anti-aliasing a box-shaped sdf ("low-res" effect created by floor()ing the sample-position of each pixel) (shader link).

For hexagons, we can thus render outlines of thickness th in hex-space by transforming our proximity measure with sdf = (0.5 - proximity) * 2.0 - th. Thus, sdf < 0 is the interior of the boundary line, and sdf > 0 is the rest of the screen. Spaced hexagons are almost as simple: sdf = abs((0.5 - proximity) * 2.0 - spacing) - th uses abs() to denote a region of pixels at the boundary of our spaced hexagons, rather than the "true" boundary.

These hexagon variations are constructed by simple manipulations of the distance function (shader link).

The right-most example above is a way of showing how this SDF approach is highly generalizable. SDF functions can have their inputs and outputs transformed, and they can be combined to create any shape. The kishimisu tutorial shows the power of transforming the "input space" when rendering, but in my opinion this Inigo Quilez (IQ) article is the best illustration of the power of combining SDFs. A smooth human face made of mathematical circles and ovals! Pythagoras would be amazed. Of course, in the case of our rounded hexes, we have simply interpolated between a circle and a hex at the corners.

A procedural field of hexes (again) (shader link).

As a celebration of our new technique, I want to return to the header image of this article! We can now see that the toHex() function allows the hex colors to be selected, and how proximity in the form of hex.w is used for everything from the interior gradients to the outlines between the hexes. Because it's an SDF, we can distort the entire image by distorting the inputs. And because it's a shader, we can animate things in hex space!

My very last word will be on the merits of using cube coordinates in rendering¹. Cube coordinates are incredible for gameplay, and there are advantages to being able to easily interpret gameplay data in your procedural rendering. In fact, when I first saw the need for "proximity", it was in the creation of this old prototype:

This screenshot is noisy, so I set saturation to 0. But, the hexes are rendering on the hills of the terrain surface directly -- a good excuse for procedural rendering if I've ever seen one!

(Bug-free UI in Unity) Next >